“How many packaging samples should I test?” For many medical device packaging professionals, this is a common question without an easy answer. Packaging test methods rarely contain sample size guidance, so it is left to the individual manufacturer to determine and justify an appropriate sample size.

Sample size justifications should be based on statistically valid rational and risk assessments. Unfortunately, there is no “magic number” that is right for every situation. For this article, we will use a commonly accepted approach to determine a sample size and discuss some special considerations to remember when doing sample size justifications.

Step 1

Usually, the first step in selecting an adequate sample size is to calculate risk. Risk is the, “combination of occurrence of harm and the severity of that harm that can occur due to failure (ISO 14971).” A common approach to calculating risk is known as a Risk Priority Number (RPN). The RPN is a calculation based on an assigned severity, occurrence and detection value. Each category is assigned a value ranging from 1 to 10. It is important to recognize that other ranges are also acceptable (that is, 1 to 5) to use when establishing the risk value.

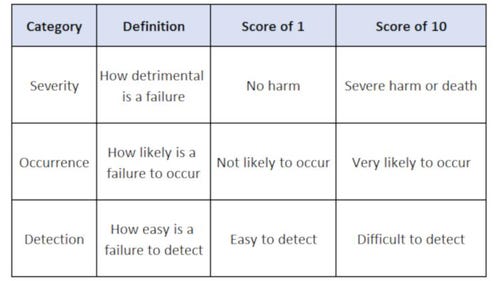
Table 1: RPN categories and definitions

The product is evaluated and a number (1-10) is assigned for each category. These values are multiplied together to calculate the RPN. You can then categorize the RPN as Low, Medium or High Risk. The RPN is not a measurement of the manufacturer’s risk; rather, it is an assignment of risk priority.

For example, in a product that has a high Severity level (such as a failure could end with catastrophic injury), a rating of 10 can be issued, which is worst case. The same product may also have a high Detection rating (where a failure is difficult to spot) so a value of 8 is assigned. Finally, it is assumed that a failure is rare and does not occur often. Therefore, an Occurrence level of 4 is assigned. These values are then multiplied together for an RPN of 320, which is a Medium Risk priority. In this example a 95% Confidence / 95% Reliability level would be assigned (Table 2).

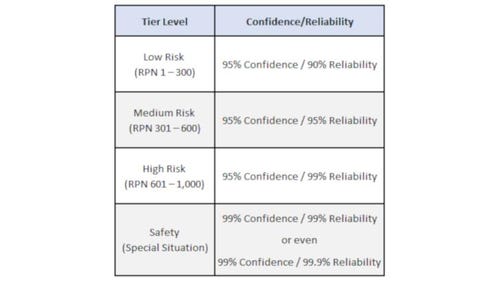
Table 2: Example of correlating Risk (RPN) to Confidence and Reliability. ISO 14971:2007 (R2016) directs us to establish these values using a 3 x 3 risk matrix. The values are examples using a range of 1-10. These would change if the range was 1-5 or 1-3.

The Confidence Interval is an expression of uncertainty about an unknown constant. Reliability is how many units will successfully meet the pass/fail criteria.

For example, a 90% reliability means that 90 out of 100 units will successfully meet all pass/fail criteria, and a 95% Confidence Interval, indicates that a manufacturer is 95% confident that they will have less than or equal to 10 true failures.

A Method 1 Non-parametric Binomial Reliability chart (Table 3) can be used to determine a minimum sample size based on Confidence/Reliability. Non-parametric binomial reliability demonstration tests are used widely for test methods that generate attribute or qualitative data.

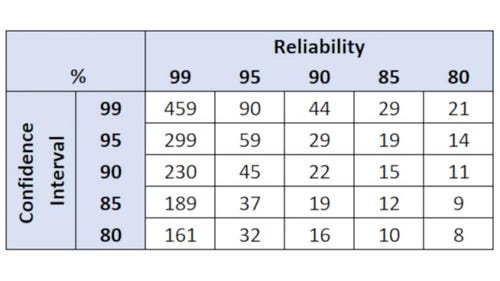
Table 3: This is just one example of Non-parametric Binomial Reliability chart with zero (0) allowable failures. Many options and processes exist for determining this. Search the internet for binomial parametric distribution and then identify how many failures are acceptable.

In our hypothetical example of an RPN of 320 and a 95%/95% Confidence/Reliability level, we would select a sample size of 59 with zero allowable failures. When incorporating allowable test failures into the equation, the sample size required to achieve the same confidence and reliability intervals increases significantly.

Other considerations

Finally, there are a number of additional factors that can also affect sample size.

• Product cost and availability can be prohibitive to larger sample sizes. Facsimile product (similar in shape, materials and weight) may need to be used when product is expensive or not readily available.

• More complex products or products that do not have a long manufacturing history may be considered a higher risk for defects and may require larger sample sets. Some products have higher inherent risks to patients. As patient risk increases, so should sample sizes.

• The test methods chosen can also affect the sample size. Generally, qualitative methods should have a larger sample set than quantitative methods. Also, depending on the type of device and packaging components, different test methods may or may not be appropriate.

Selecting an appropriate sample size can be complex as there are many factors to consider, and no single approach will be appropriate 100% of the time. There are multiple approaches to determining risk, and risk assessment is usually not simple and straight forward. It is important to have qualified people who understand your device, how the device will be used, how to appropriately determine risk, which test methods would be suitable for your device and how to build a statistically valid sampling plan. A packaging expert and a statistician can be valuable partners in helping you select and justify your sampling plan.